数据结构与算法-跳跃表
 2020-07-24  d389ec10c5af45b618f23d5a8c8cd701 99+   5 分钟   0.8 k  0次访问

数据结构与算法-跳跃表

假如我们要用某种数据结构来维护一组有序的 int 型数据的集合，并且希望这个数据结构在插入、删除、查找等操作上能够尽可能的快速，那么，你会用什么样的数据结构呢？

一、数组

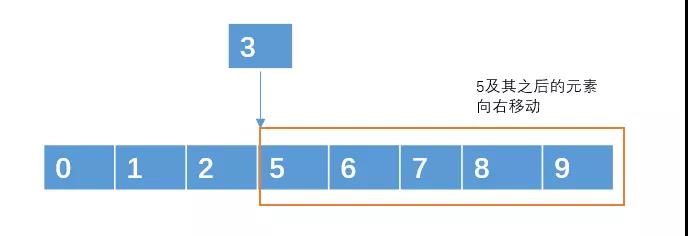
一种很简单的方法应该就是采用数组了，在查找方面，用数组存储的话，采用二分法可以在 O(logn) 的时间里找到指定的元素，不过数组在插入、删除这些操作中比较不友好，找到目标位置所需时间为 O(logn)，进行插入和删除这个动作所需的时间复杂度为 O(n)，因为都需要移动元素，所以最终所需要的时间复杂度为 O(n)。

例如对于下面这个数组：

插入元素 3

二、链表

另外一种简单的方法应该就是用链表了，链表在插入、删除的支持上就相对友好，当我们找到目标位置之后，插入、删除元素所需的时间复杂度为 O(1)，注意，我说的是找到目标位置之后，插入、删除的时间复杂度才为 O(1)。

但链表在查找上就不友好了，不能像数组那样采用二分查找的方式，只能一个一个结点遍历，所以加上查找所需的时间，插入、删除所需的总的时间复杂度为 O(n)。

假如我们能够提高链表的查找效率，使链表的查找的时间复杂度尽可能接近 O(logn)，那链表将会是很棒的选择。

三、提高链表的查找速度

那链表的查找速度可以提高吗？

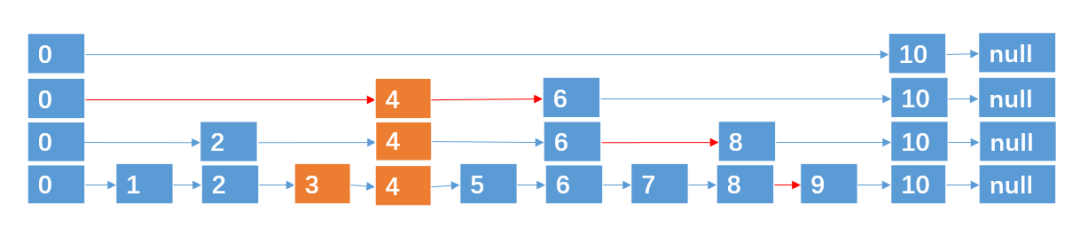
对于下面这个链表：

假如我们要查找元素 9，按道理我们需要从头结点开始遍历，一共遍历 8 个结点才能找到元素 9。能否采取某些策略，让我们遍历 5 次以内就找到元素 9 呢？请大家花一分钟时间想一下如何实现？

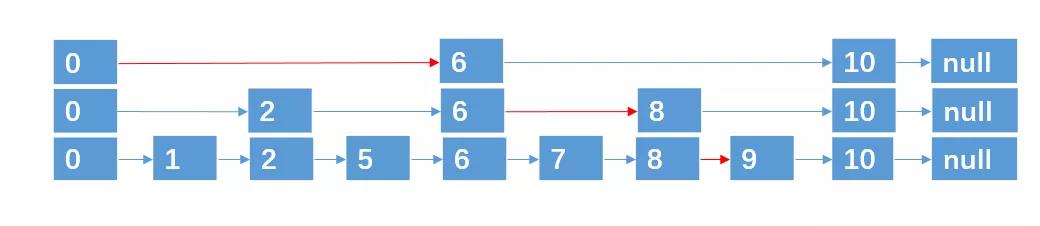
由于元素的有序的，我们是可以通过增加一些路径来加快查找速度的。

通过这种方法，我们只需要遍历 5 次就可以找到元素 9 了（红色的线为查找路径）。

还能继续加快查找速度吗？

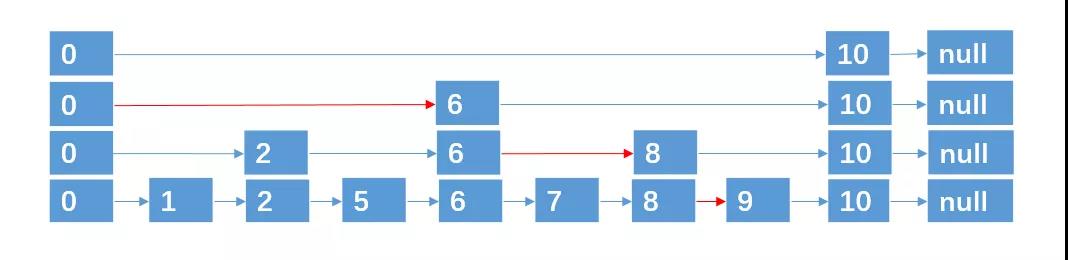
答案是可以的，再增加一层就行了，这样只需要 4 次就能找到了，这就如同我们搭地铁的时候，去某个站点时，有快线和慢线几种路线，通过快线 + 慢线的搭配，我们可以更快找到达某个站点。

当然，还能再增加一层

基于这种方法，对于具有 n 个元素的链表，我们可以采取（O(logn) + 1)）层指针路径的形式，就可以实现在 O(logn) 的时间复杂度内，查找到某个目标元素了，这种数据结构，我们也称之为跳跃表，跳跃表也可以算是链表的一种变形，只是它具有二分查找的功能。

四、插入与删除

上面例子中，9 个结点，一共 4 层，可以说是理想的跳跃表了，不过随着我们对跳跃表进行插入/删除结点的操作，那么跳跃表结点数就会改变，意味着跳跃表的层数也会动态改变。

这里我们面临一个问题，就是新插入的结点应该跨越多少层？

这个问题已经有大牛替我们解决好了，采取的策略是通过抛硬币来决定新插入结点跨越的层数：每次我们要插入一个结点的时候，就来抛硬币，如果抛出来的是正面，则继续抛，直到出现负面为止，统计这个过程中出现正面的次数，这个次数作为结点跨越的层数。

通过这种方法，可以尽可能的接近理想的层数。大家可以想一下为什么会这样呢？

4.1、插入

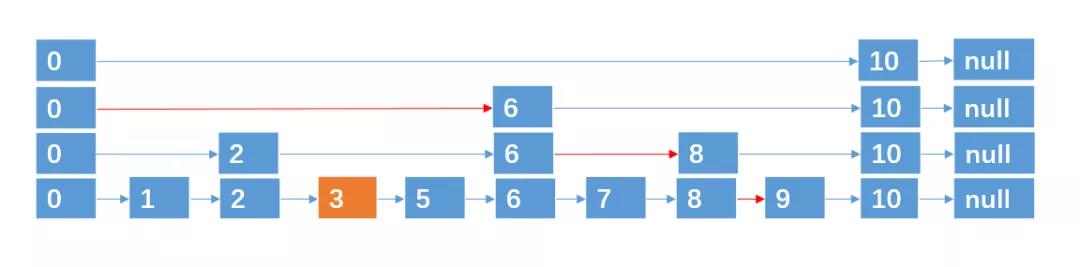
例如，我们要插入结点 3、4，通过抛硬币知道 3、4 跨越的层数分别为 0、2 (层数从 0 开始算)，则插入的过程如下

插入 3，跨越 0 层

插入 4，跨越 2 层

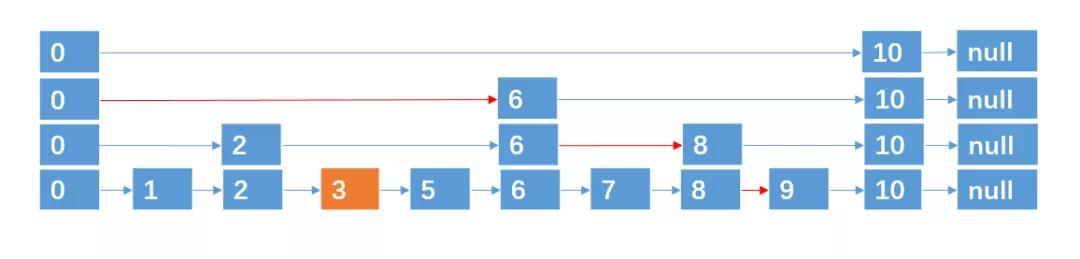
4.2、删除

解决了插入之后，我们来看看删除，删除就比较简单了，例如我们要删除 4，那我们直接把 4 及其所跨越的层数删除就行了。

五、小结

总结下跳跃表的有关性质：

(1). 跳跃表的每一层都是一条有序的链表。

(2). 跳跃表的查找次数近似于层数，时间复杂度为 O(logn)，插入、删除也为 O(logn)。

(3). 最底层的链表包含所有元素。

(4). 跳跃表是一种随机化的数据结构（通过抛硬币来决定层数）。

(5). 跳跃表的空间复杂度为 O(n)。

5.1、跳跃表 vs 二叉查找树

有人可能会说，也可以采用二叉查找树啊，因为二叉查找树的插入、删除、查找也是近似 O(logn) 的时间复杂度。

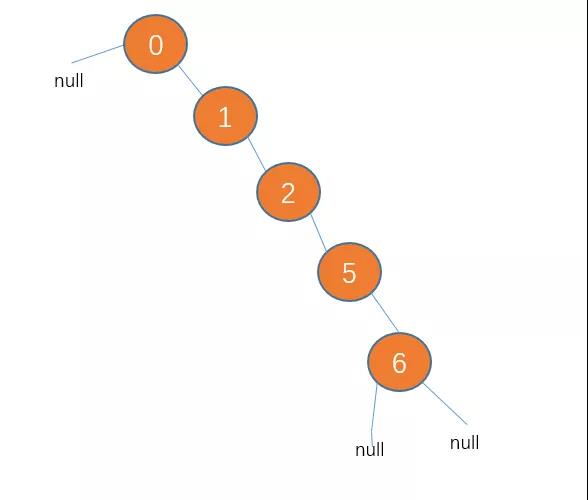
不过，二叉查找树是有可能出现一种极端的情况的，就是如果插入的数据刚好一直有序，那么所有节点会偏向某一边。

这种结构会导致二叉查找树的查找效率变为 O(n)，这会使二叉查找树大打折扣。

5.2、跳跃表 vs 红黑树

红黑树可以说是二叉查找树的一种变形，红黑树在查找、插入，删除也是近似 O(logn) 的时间复杂度。

而且红黑树插入，删除结点时，是通过调整结构来保持红黑树的平衡，比起跳跃表直接通过一个随机数来决定跨越几层，在时间复杂度的花销上是要高于跳跃表的。

当然，红黑树并不是一定比跳跃表差，在有些场合红黑树会是更好的选择，所以选择一种数据结构，关键还得看场合。

总上所述，维护一组有序的集合，并且希望在查找、插入、删除等操作上尽可能快，那么跳跃表会是不错的选择。redis 中的某些数据结构便是采用了跳跃表，当然，redis 也结合了哈希表等数据结构，采用的是一种复合数据结构。

5.3、小结

跳表是一种可以替代平衡树的数据结构。跳表追求的是概率性平衡，而不是严格平衡。因此，跟平衡二叉树相比，跳表的插入和删除操作要简单得多，执行也更快。

Skiplist 的复杂度和红黑树一样，而且实现起来更简单。在并发环境下 Skiplist 有另外一个优势，红黑树在插入和删除的时候可能需要做一些 rebalance 的操作，这样的操作可能会涉及到整个树的其他部分，而 Skiplist 的操作显然更加局部性一些，需要关注的节点更少，因此在这样的情况下性能好一些。

六、代码实现

Java 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
 //节点
 class Node{
      int value = -1;
      int level;//跨越几层
      Node[] next;//指向下一个节点
  
      public Node(int value, int level) {
          this.value = value;
          this.level = level;
          this.next = new Node[level];
     }
  }
  //跳跃表
  public class SkipList {
     //允许的最大层数
     int maxLevel = 16;
     //头节点，充当辅助。
     Node head = new Node(-1, 16);
     //当前跳跃表节点的个数
     int size = 0;
     //当前跳跃表的层数,初始化为1层。
     int levelCount = 1;
 
     public Node find(int value) {
         Node temp = head;
         for (int i = levelCount - 1; i >= 0; i--) {
             while (temp.next[i] != null && temp.next[i].value < value) {
                 temp = temp.next[i];
             }
         }
         //判断是否有该元素存在
         if (temp.next[0] != null && temp.next[0].value == value) {
             System.out.println(value + "  查找成功");
             return temp.next[0];
         } else {
             return null;
         }
     }
     //为了方便，跳跃表在插入的时候，插入的节点在当前跳跃表是不存在的
     //不允许插入重复数值的节点。
     public void insert(int value) {
         int level = getLevel();
         Node newNode = new Node(value, level);
         //update用于记录要插入节点的前驱
         Node[] update = new Node[level];
         
         Node temp = head;
         for (int i = level - 1; i >= 0; i--) {
             while (temp.next[i] != null && temp.next[i].value < value) {
                 temp = temp.next[i];
             }
             update[i] = temp;
         }
         //把插入节点的每一层连接起来
         for (int i = 0; i < level; i++) {
             newNode.next[i] = update[i].next[i];
             update[i].next[i] = newNode;
         }
         //判断是否需要更新跳跃表的层数
         if (level > levelCount) {
             levelCount = level;
         }
         size++;
         System.out.println(value + " 插入成功");
     }
 
     public void delete(int value) {
         Node[] update = new Node[levelCount];
         Node temp = head;
 
         for (int i = levelCount - 1; i >= 0; i--) {
             while (temp.next[i] != null && temp.next[i].value < value) {
                 temp = temp.next[i];
             }
             update[i] = temp;
         }
 
         if (temp.next[0] != null && temp.next[0].value == value) {
             size--;
             System.out.println(value + " 删除成功");
             for (int i = levelCount - 1; i >= 0; i--) {
                 if (update[i].next[i] != null && update[i].next[i].value == value) {
                     update[i].next[i] = update[i].next[i].next[i];
                 }
             }
         }
     }
 
     //打印所有节点
     public void printAllNode() {
         Node temp = head;
         while (temp.next[0] != null) {
             System.out.println(temp.next[0].value + "  ");
             temp = temp.next[0];
         }
     }
 
     //模拟抛硬币
    private int getLevel() {
        int level = 1;
        while (true) {
            int t = (int)(Math.random() * 100);
            if (t % 2 == 0) {
                level++;
            } else {
                break;
            }
        }
        System.out.println("当前的level = " + level);
        return level;
    }

    //测试数据
    public static void main(String[] args) {
        SkipList list = new SkipList();
        for (int i = 0; i < 6; i++) {
            list.insert(i);
        }
        list.printAllNode();
        list.delete(4);
        list.printAllNode();
        System.out.println(list.find(3));
        System.out.println(list.size + " " + list.levelCount);
    }
}

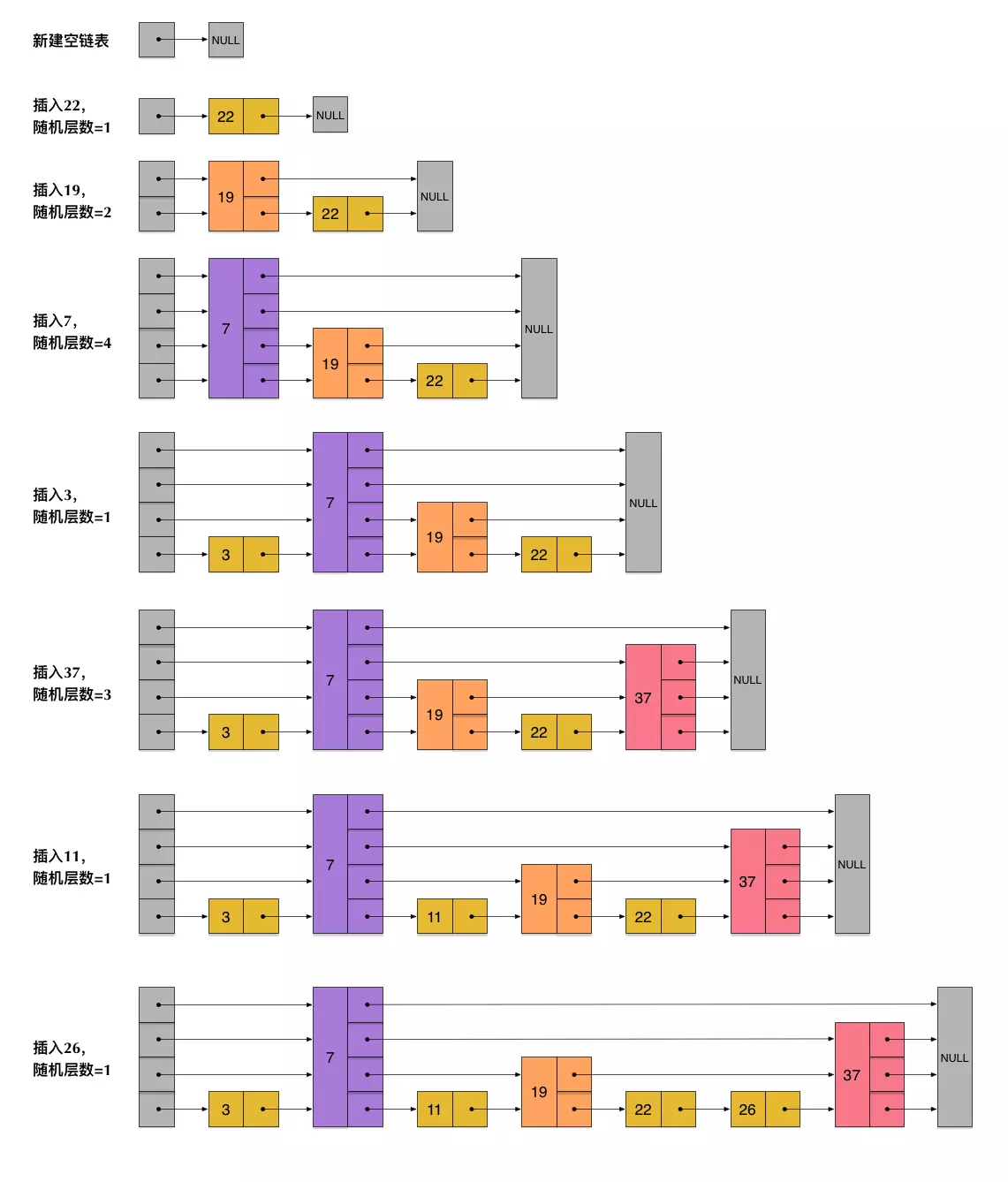
跳跃表构造图示

C++ 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
#ifndef SKIPLIST_H
#define SKIPLIST_H

#include <ctime>
#include <initializer_list>
#include <iostream>
#include <random>

template <typename Key>
class Skiplist
{
    public:
        struct Node
        {
            Node(K k) : key(k) {}
            Key key;
            Node* next[1];  // C 语言中的柔性数组技巧
        };

    private:
        int maxLevel;
        Node* head;

        enum { kMaxLevel = 12 };

    public:
        Skiplist() : maxLevel(1)
        {
            head = newNode(0, kMaxLevel);
        }
        
        Skiplist(std::initializer_list<Key> init) : Skiplist()
        {
            for(const Key& k : int)
            {
                insert(k);
            }
        }

        ~Skiplist()
        {
            Node* pNode = head;
            Node* delNode;
            while(nullptr != pNode)
            {
                delNode = pNode;
                pNode = pNode->next[0];
                free(delNode);  // 对应 malloc
            }
        }

        // 禁止拷贝构造和赋值构造
        Skiplist(const Skiplist&) = delete;
        Skiplist& operator=(const Skiplist&) = delete;
        Skiplist& operator=(Skiplist&&) = delete;


    private:
        Node* newNode(const Key& key, int level)
        {
            /*
                开辟 sizeof(Node) + sizeof(Node*) * (level - 1) 大小的空间
                sizeof(Node*) * (level - 1) 大小的空间是给 Node.next[1] 指针数组用的
                为什么是 level - 1 而不是 level，因为 sizeof(Node) 已包含一个 Node* 指针的空间
            */
            void* node_memory = malloc(sizeof(Node) + sizeof(Node*) * (level - 1));
            Node* node = new (node_memory) Node(Key);
            for(int i = 0; i < level; ++i)
            {
                node->next[i] = nullptr;
            }

            return node;
        }

        // 随机函数，范围 [1, kMaxLevel]，越小概率越大
        static int randomLevel()
        {
            int level = 1;
            while(rand() % 2 && level < kMaxLevel)
            {
                level++;
            }
            return level;
        }

    public:
        Node* find(const Key* key)
        {
            // 从最高层开始查找，每层查找最后一个小于 key 的前驱节点，不断缩小范围
            Node* pNode = head;
            for(int i = maxLevel - 1; i >= 0; --i)
            {
                while(pNode->next[i] != nullptr && pNode->next[i]->key < key)
                {
                    pNode = pNode->next[i];
                }
            }

            // 如果第一层的 pNode[0]->key == key，则返回 pNode->next[0]，即找到 key
            if(nullptr != pNode->next[0] && pNode->next[0]->key == key)
            {
                return pNode->next[0];
            }

            return nullptr;
        }

        void insert(const Key& key)
        {
            int level = randomLevel();
            Node* new_node = newNode(key, level);
            Node* prev[kMaxLevel];
            Node* pNode = head;
            // 从最高层开始查找，每层查找最后一个小于 key 的前继节点
            for(int i = level - 1; i >= 0; --i)
            {
                while(pNode->next[i] != nullptr && pNode->next[i]->key < key)
                {
                    pNode = pNode->next[i];
                }
                prev[i] = pNode;
            }
            // 然后每层将新节点插入到前继节点后面
            for(int i = 0; i < level; ++i)
            {
                new_node->next[i] = prev->next[i];
                prev[i]->next[i] = new_node;
            }

            if(maxLevel < level)    // 层数大于最大层数，更新最大层数
            {
                maxLevel = level;
            }
        }

        void erase(const Key& key)
        {
            Node* prev[maxLevel];
            Node* pNode = head;
            // 从最高层开始查找，每层查找最后一个小于 key 的前继节点
            for(int i = maxLevel - 1; i >= 0; --i)
            {
                while(pNode->next[i] != nullptr && pNode->next[i]->key < key)
                {
                    pNode = pNode->next[i];
                }
                prev[i] = pNode;
            }

            // 如果找到 key
            if(pNode->next[0] != nullptr && pNode->next[0]->key == key)
            {
                Node* delNode = pNode->next[0];
                // 从最高层开始，如果当前层的 next 节点的值等于 key，则删除 next 节点
                for(int i = maxLevel - 1; i >= 0; --i)
                {
                    if(prev[i]->next[i] != nullptr && key == prev[i]->next[i]->key)
                    {
                        prev[i]->next[i] = prev[i]->next[i]->next[i];
                    }
                }
                free(delNode);  // 最后销毁 pNode->next[0] 节点
            }

            // 如果 maxLevel > 1 且头结点的 next 指针为空，则该层已无数据，maxLevel 减 1
            while(maxLevel > 1 && head->next[maxLevel] == nullptr)
            {
                maxLevel--;
            }
        }
};

#endif

初始化列表参考
C++11新特性-初始化列表initializer_list

参考原文:
以后有面试官问你「跳跃表」，你就把这篇文章扔给他

喜欢这篇文章？打赏一下作者吧

评论

目录

关注我

:D 一言句子获取中...

最新评论

加载中，最新评论有1分钟缓存...

最新文章

分类

归档

标签

C++18
数据结构7
计算机网络5
TCP4
字符串4
数学4
算法4
Golang3
epoll3
golang3
leetcode3
操作系统3
服务器3
线程3
设计模式3
进程3
链表3
面向对象3
Go2
go2
查看全部>>

订阅更新

输入邮箱开始订阅，更博后邮件通知！