二叉搜索树
一、什么是二叉搜索树
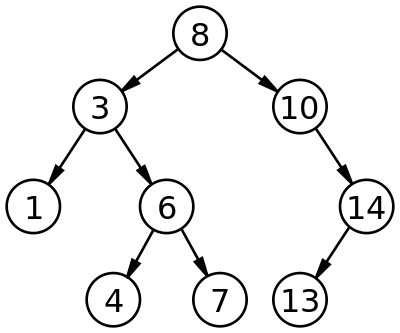
二叉搜索树(binary search tree, BST)也叫排序的二叉树,根节点比左边子树的所有节点都大,比右边子树上的所有节点都小,如下图就是一个二叉搜索树:

要实现一个二叉搜索树,我们需要实现节点的插入和删除,要实现节点的查找(搜索),要实现前序遍历、中序遍历和后序遍历,要实现最大节点和最小节点的查找。
二、定义基本数据结构
常规地,我们定义节点的类型,每个节点包含它的值以及左右节点。因为目前 Go 泛型还没有发布,所以这里我们实现一个元素为 int 类型的具体的二叉搜索树,等泛型实现后可以改成抽象的二叉搜索树。
树只要包含根节点可以了。
1
2
3
4
5
6
7
8
9
10
11
|
type Node struct {
value int
left *Node
right *Node
}
type BST struct {
root *Node
}
|
三、插入和删除
既然是一棵树,就需要增加节点用来构造树,大部分情况下也需要删除节点。
增加节点的时候,需要判断应该往左边子树上添加,还是往右边子树上添加。天然地,既然二叉搜索树是一个有序的,那么我们就可以进行比较,然后递归的实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
func (bst *BST) Insert(value int) {
newNode := &Node{value, nil, nil}
if bst.root == nil {
bst.root = newNode
} else {
insertNode(bst.root, newNode)
}
}
func insertNode(root, newNode *Node) {
if newNode.value < root.value {
if root.left == nil {
root.left = newNode
} else {
insertNode(root.left, newNode)
}
} else if newNode.value > root.value {
if root.right == nil {
root.right = newNode
} else {
insertNode(root.right, newNode)
}
}
}
|
删除有些麻烦,如果是删除叶节点就比较容易,删除即可。但是如果不是删除叶节点,那么就需要将子节点提升。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
func (bst *BST) Remove(value int) bool {
_, existed := remove(bst.root, value)
return existed
}
func remove(root *Node, value int) (*Node, bool) {
if root == nil {
return nil, false
}
var existed bool
if value < root.value {
root.left, existed = remove(root.left, value)
return root, existed
}
if value > root.value {
root.right, existed = remove(root.right, value)
return root, existed
}
existed = true
if root.left == nil && root.right == nil {
root = nil
return root, existed
}
if root.left == nil {
root = root.right
return root, existed
}
if root.right == nil {
root = root.left
return root, existed
}
smallestInRight, _ := min(root.right)
root.value = smallestInRight
root.right, _ = remove(root.right, smallestInRight)
return root, existed
}
|
四、搜索
检查一个节点是否存在比较简单,因为二叉搜索树是有序的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func (bst *BST) Search(value int) bool {
return search(bst.root, value)
}
func search(n *Node, value int) bool {
if n == nil {
return false
}
if value < n.value {
return search(n.left, value)
}
if value > n.value {
return search(n.right, value)
}
return true
}
|
同时,我们还可以实现查找一个二叉搜索树的最大最小值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
func (bst *BST) Min() (int, bool) {
return min(bst.root)
}
func min(node *Node) (int, bool) {
if node == nil {
return 0, false
}
n := node
for {
if n.left == nil {
return n.value, true
}
n = n.left
}
}
func (bst *BST) Max() (int, bool) {
return max(bst.root)
}
func max(node *Node) (int, bool) {
if node == nil {
return 0, false
}
n := node
for {
if n.right == nil {
return n.value, true
}
n = n.right
}
}
|
五、遍历
可以实现先序遍历、中序遍历和后序遍历,先中后指的是根节点相对子节点的处理顺序。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
func (bst *BST) PreOrderTraverse(f func(int)) {
preOrderTraverse(bst.root, f)
}
func preOrderTraverse(n *Node, f func(int)) {
if n != nil {
f(n.value)
preOrderTraverse(n.left, f)
preOrderTraverse(n.right, f)
}
}
func (bst *BST) PostOrderTraverse(f func(int)) {
postOrderTraverse(bst.root, f)
}
func postOrderTraverse(n *Node, f func(int)) {
if n != nil {
postOrderTraverse(n.left, f)
postOrderTraverse(n.right, f)
f(n.value)
}
}
|
参考原文:
用Go撸一个二叉搜索树