数据结构与算法-二分查找
 2020-07-30  4041c2a8ca711ea5830aef9ed7eed28d 99+   2 分钟   0.3 k  0次访问

数据结构与算法-二分查找

二分查找

零、二分查找实例-定位 IP 对应省份

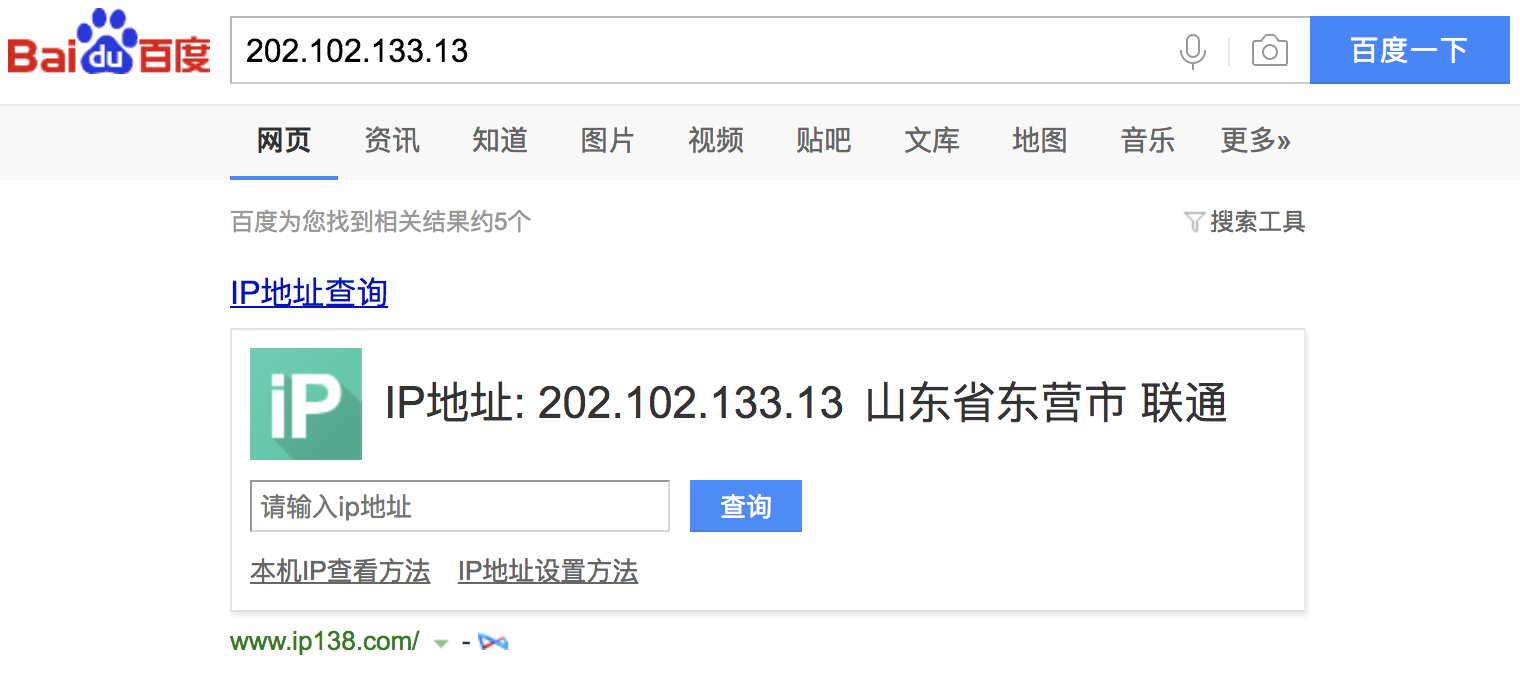
通过 IP 地址来查找 IP 归属地功能，不知道你用过没？没用过也没关系，打开百度，在搜索框里随便输入一个 IP 地址，就会看到它的归属地。

这个功能并不复杂，它是通过维护一个很大的 IP 地址库来实现。地址库中包括 IP 地址范围和归属地的对应关系。

当我们想要查询 202.102.133.13 这个 IP 地址的归属地时，我们就在地址库中搜索，发到 IP 地址落在[202.102.133.0, 202.102.133.255] 这个地址范围内，那我们就可以将这个 IP 地址范围对应的归属地“山东东营市”显示给用户了。

1
2
3
4
5
6
[202.102.133.0, 202.102.133.255]  山东东营市 
[202.102.135.0, 202.102.136.255]  山东烟台 
[202.102.156.34, 202.102.157.255] 山东青岛 
[202.102.48.0, 202.102.48.255] 江苏宿迁 
[202.102.49.15, 202.102.51.251] 江苏泰州 
[202.102.56.0, 202.102.56.255] 江苏连云港

现在我的问题是，在庞大地址库中逐一比对 IP 地址所在的区间，是非常耗时的。假设我们有 12 万条这样的 IP 区间与归属地的对应关系，如何快速出一个 IP 地址的归属地呢？

唐纳德·克努特（Donald E.Knuth）在《计算机程序设计艺术》的第 3 卷《排序和查找》中说到：“尽管第一个二分查找算法于 1946 年出现，然而第一个完全正确的二分查找算法实现直到 1962 年才出现。”

二分查找的变形问题很多。

一、查找第一个值等于给定值的元素

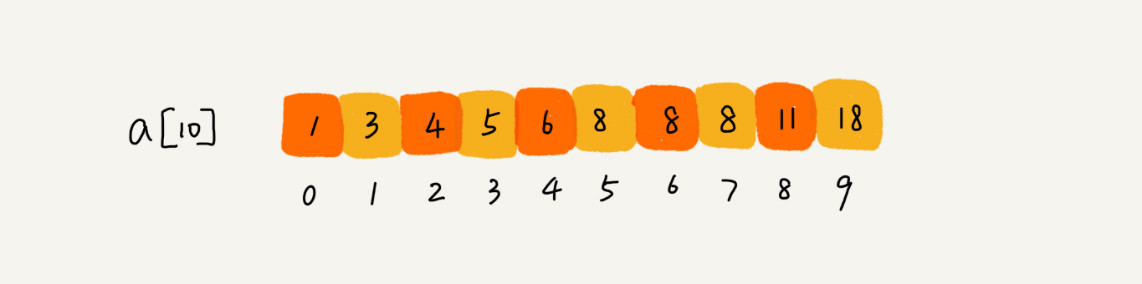
如果有序数据集合中存在重复的数据，我们希望找到第一个值等于给定值的数据。

比如下面这样一个有序数组，其中 a[5]，a[6]，a[7] 的值都等于 8，是重复的数据。我们希望查找第一个等于 8 的数据，也就是下标是 5 的元素。

1、写法一

100 个人写二分查找就会有 100 种写法。网上有很多关于变形二分查找的实现方法，有很多写得非常简洁，比如下面这个写法。但是，尽管简洁，理解起来却非常烧脑，也很容易写错。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid = low + ((high - low) >> 1);
    if (a[mid] >= value) {
      high = mid - 1;
    } else {
      low = mid + 1;
    }
  }

  if (low < n && a[low]==value) return low;
  else return -1;
}

2、方法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

a[mid] 跟要查找的 value 的大小关系有三种情况：大于、小于、等于。对于 a[mid] > value 的情况，我们需要更新 high = mid-1；对于 a[mid] < value 的情况，我们需要更新 low = mid+1。那当 a[mid] = value 的时候应该如何处理呢？

如果我们查找的是任意一个值等于给定值的元素，当 a[mid] 等于要查找的值时，a[mid] 就是我们要找的元素。但是，如果我们求解的是第一个值等于给定值的元素，当 a[mid] 等于要查找的值时，我们就需要确认一下这个 a[mid] 是不是第一个值等于给定值的元素。

我们重点看第 11 行代码。如果 mid 等于 0，那这个元素已经是数组的第一个元素，那它肯定是我们要找的；如果 mid 不等于 0，但 a[mid] 的前一个元素 a[mid-1] 不等于 value，那也说明 a[mid] 就是我们要找的第一个值等于给定值的元素。

如果经过检查之后发现 a[mid] 前面的一个元素 a[mid-1] 也等于 value，那说明此时的 a[mid] 肯定不是我们要查找的第一个值等于给定值的元素。那我们就更新 high = mid-1，因为要找的元素肯定出现在 [low, mid-1] 之间。

对比上面的两段代码，是不是下面那种更好理解？实际上，很多人都觉得变形的二分查找很难写，主要原因是太追求第一种那样完美、简洁的写法。而对于我们做工程开发的人来说，代码易读懂、没 Bug，其实更重要，所以我觉得第二种写法更好。

3、方法三

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 查找第一个等于给定值的元素
private int binarySearchFirst(int[] a, int value) {
	int n = a.length;
	int low = 0;
	int high = n - 1;
	while (low <= high) {
		int mid = (low + high) / 2;
		if (a[mid] == value) {
			if (a[low] == value) {
				return low;
			}
			if(a[mid - 1] != value) {
				return mid;
			}else {
				high = mid -1;
			}
		} else if (a[mid] < value) {
			low = mid + 1;
		} else {
			high = mid - 1;
		}
	}
	return -1;
}

二、查找最后一个等于给定值的元素

1、方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

我们还是重点看第 11 行代码。如果 a[mid] 这个元素已经是数组中的最后一个元素了，那它肯定是我们要找的；如果 a[mid] 的后一个元素 a[mid+1] 不等于 value，那也说明 a[mid] 就是我们要找的最后一个值等于给定值的元素。

如果我们经过检查之后，发现 a[mid] 后面的一个元素 a[mid+1] 也等于 value，那说明当前的这个 a[mid] 并不是最后一个值等于给定值的元素。我们就更新 low = mid+1，因为要找的元素肯定出现在 [mid+1, high] 之间。

2、方法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 查找最后一个等于给定值的元素
private int binarySearchLast(int[] a, int value) {
	int n = a.length;
	int low = 0;
	int high = n - 1;
	while (low <= high) {
		int mid = (low + high) / 2;
		if (a[mid] == value) {
			if (a[high] == value) {
				return high;
			}
			if(a[mid + 1] != value) {
				return mid;
			}else {
				low = mid + 1;
			}
		} else if (a[mid] < value) {
			low = mid + 1;
		} else {
			high = mid - 1;
		}
	}
	return -1;
}

三、查找第一个大于等于给定值的元素

现在我们再来看另外一类变形问题。在有序数组中，查找第一个大于等于给定值的元素。比如，数组中存储的这样一个序列：3，4，6，7，10。如果查找第一个大于等于 5 的元素，那就是 6。

1、方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] >= value) {
      if ((mid == 0) || (a[mid - 1] < value)) return mid;
      else high = mid - 1;
    } else {
      low = mid + 1;
    }
  }
  return -1;
}

如果 a[mid] 小于要查找的值 value，那要查找的值肯定在 [mid+1, high] 之间，所以，我们更新 low = mid+1。

对于 a[mid] 大于等于给定值 value 的情况，我们要先看下这个 a[mid] 是不是我们要找的第一个值大于等于给定值的元素。如果 a[mid] 前面已经没有元素，或者前面一个元素小于要查找的值 value，那 a[mid] 就是我们要找的元素。这段逻辑对应的代码是第 7 行。

如果 a[mid-1] 也大于等于要查找的值 value，那说明要查找的元素在 [low, mid-1] 之间，所以，我们将 high 更新为 mid-1。

2、方法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 第一个大于等于
private int greaterOrEqualFirst(int[]a, int value) {
	int n = a.length;
	int low = 0;
	int high = n -1;
	// 判断首尾元素与value的大小关系
	if(value <= a[low]) {
		return low;
	}
	if(value > a[high]) {
		return -1;
	}
	// 进入循环之后，保证 a[low] < value <= a[high]
	while(low + 1 != high) {
		int mid = (low + high) / 2;
		if(a[mid] >= value) {
			high = mid + 1 ;
		}else {
			low = mid + 1;
		}
	}
	return high;
}

四、查找最后一个小于等于给定值的元素

现在，我们来看最后一种二分查找的变形问题，查找最后一个小于等于给定值的元素。比如，数组中存储了这样一组数据：3，5，6，8，9，10。最后一个小于等于 7 的元素就是 6。是不是有点类似上面那一种？实际上，实现思路也是一样的。

1、方法一

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int bsearch7(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] > value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

2、方法二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 最后一个小于等于
private int lessOrEqualLast(int[]a, int value) {
	int n = a.length;
	int low = 0;
	int high = n -1;
	if(value < a[low]) {
		return -1;
	}
	if(value >= a[high]) {
		return high;
	}
	while(low + 1 != high) {
		int mid = (low + high) / 2;
		if(a[mid] <= value) {
			low = mid + 1;
		}else {
			high = mid + 1;
		}
	}
	return low;
}

五、IP 问题解答

如何快速定位出一个 IP 地址的归属地？

现在这个问题应该很简单了。如果 IP 区间与归属地的对应关系不经常更新，我们可以先预处理这 12 万条数据，让其按照起始 IP 从小到大排序。如何来排序呢？我们知道，IP 地址可以转化为 32 位的整型数。所以，我们可以将起始地址，按照对应的整型值的大小关系，从小到大进行排序。

然后，这个问题就可以转化为第四种变形问题“在有序数组中，查找最后一个小于等于某个给定值的元素”了。

当我们要查询某个 IP 归属地时，我们可以先通过二分查找，找到最后一个起始 IP 小于等于这个 IP 的 IP 区间，然后，检查这个 IP 是否在这个 IP 区间内，如果在，我们就取出对应的归属地显示；如果不在，就返回未查找到。

六、内容小结

凡是用二分查找能解决的，绝大部分我们更倾向于用散列表或者二叉查找树。即便是二分查找在内存使用上更节省，但是毕竟内存如此紧缺的情况并不多。那二分查找真的没什么用处了吗？

实际上，上一节讲的求“值等于给定值”的二分查找确实不怎么会被用到，二分查找更适合用在“近似”查找问题，在这类问题上，二分查找的优势更加明显。用其他数据结构，比如散列表、二叉树，就比较难实现了。

变体的二分查找算法写起来非常烧脑，很容易因为细节处理不好而产生 Bug，这些容易出错的细节有：终止条件、区间上下界更新方法、返回值选择。

参考原文:
二分查找（下）：如何快速定位IP对应的省份地址？

喜欢这篇文章？打赏一下作者吧

评论

目录

关注我

:D 一言句子获取中...

最新评论

加载中，最新评论有1分钟缓存...

最新文章

分类

归档

标签

C++18
数据结构7
计算机网络5
TCP4
字符串4
数学4
算法4
Golang3
epoll3
golang3
leetcode3
操作系统3
服务器3
线程3
设计模式3
进程3
链表3
面向对象3
Go2
go2
查看全部>>

订阅更新

输入邮箱开始订阅，更博后邮件通知！